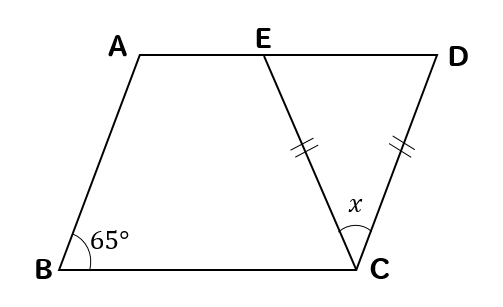
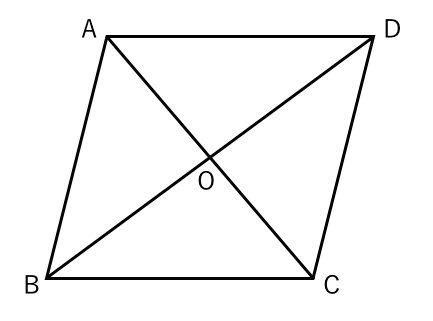
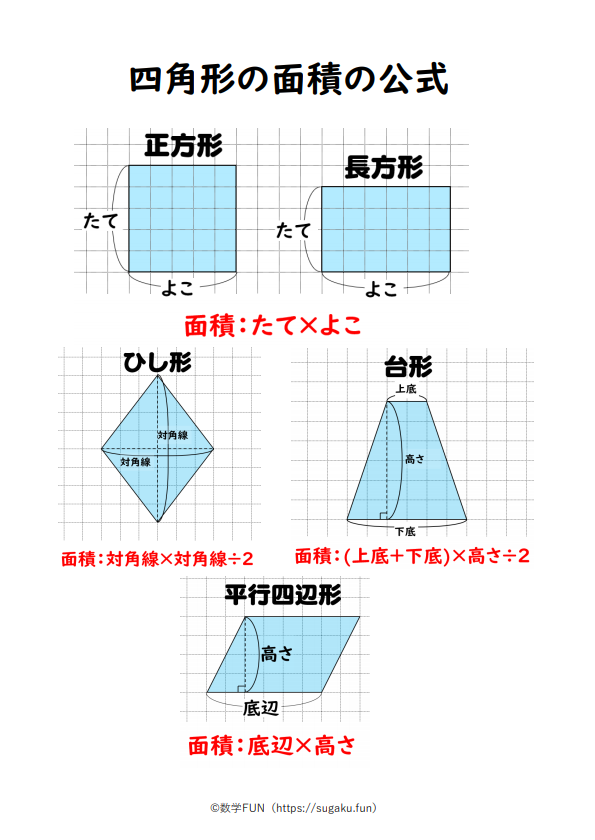
平行四辺形の対角線によって、平行四辺形を互いに合同な2つの三角形に分けることができる。 平行四辺形の面積sは 〔底辺〕×〔高さ〕 で求めることができる。これは平行四辺形を面積を変えずに長方形に変形させることで説明できる 。平行四辺形の向かい合う角は等しいので, a =110° 同様にして,四角形GDFI も平行四辺形で, b =∠DGI=180°- a =180°-110°=70° また,平行四辺形の向かい合う辺は等しいので, x =CF 7 -4 3cm, y AG 10 6 4cm 問題(後期期末)正方形、平行四辺形の詳細など下記も参考になります。 ひし形の面積は?1分でわかる求め方、公式、辺の長さ、対角線との関係 正方形の対角線は?1分でわかる値、公式、長さの計算、辺の長さとの関係 平行四辺形とは?

平行四辺形と長方形 ひし形 正方形の関係 苦手な数学を簡単に
平行四辺形 対角線 長さ 違う
平行四辺形 対角線 長さ 違う-平行四辺形において 1.対角線の長さが等しいなら長方形である. 2.対角線が直交するならひし形である. 3.対角線の長さが等しく直交するなら正方形である. 証明 1. abdと bacにおいて 3辺がそれぞれ等しいから abd≡ bac ∠a=∠b さらに,ザンダー錯視(サンダーさくし、Sander illusion)あるいはザンダーの平行四辺形(サンダーのへいこうしへんけい、Sander's parallelogram)は、ドイツの心理学者フリードリッヒ・ザンダー(Friedrich Sander, )によって1926年に報告された錯視である。 しかし、この図形はMatthew Luckieshによって彼の著書




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun
長方形は、平行四辺形の性質を満たし、加えて ・2本の対角線の長さが等しい という性質を持ちます。 正方形は、平行四辺形の性質に加えて ・対角線の長さが等しい ・対角線が垂直に交わる という性質を持ちます。平行四辺形、長方形、正方形の関係性を示しました。 まとめ1.長方形の対角線の長さは等しい。 abcと dcbで 平行四辺形なので ab=dc 1 bc=cb(共通) 2 長方形なので 1、2、3より、2辺とその間の角が、それぞれ等しいので abc≡ dcb よって ac=db <戻る台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から) 円に内接する四角形の面積(4辺から) 四角形の面積(4辺と対角の和から) 正多角形の面積 正多角形の面積から辺 円の面積
四角形 abcd において,対角線 bd , ac の中点をそれぞれ q , s ,辺 ad , bc の中点をそれぞれ p , r とする. ab=6 , bc=10 , cd=8, da=4 とするとき,次の辺の長さを求めなさい. _____ pq=rs= _____ qr=sp= (これらから四角形 pqrs は平行四辺形であることが言えます.)平行四辺形の特徴は、 ① 「2組の対辺(向かい合う辺)が、それぞれ平行」 に加えて、残り3つ。 キーワードは、 「辺」 、 「角」 、 「対角線」 だよ。 まずは、 「辺」 から。 ② 「2組の対辺がそれぞれ等しい」 向かい合う辺の長さ が、それぞれ 平行四辺形の定義↓ 2組の対辺がそれぞれ等しい。 2組の対角がそれぞれ等しい。 2組の対辺がそれぞれ平行。 2本の対角線がともに、互いの中点で交わる。 1組の対辺が平行であり、かつその長さが等しい。 です! サウラ 1年以上前 平行四辺形は2組の対辺の長さがそれぞれ等しいという性質をもっています!
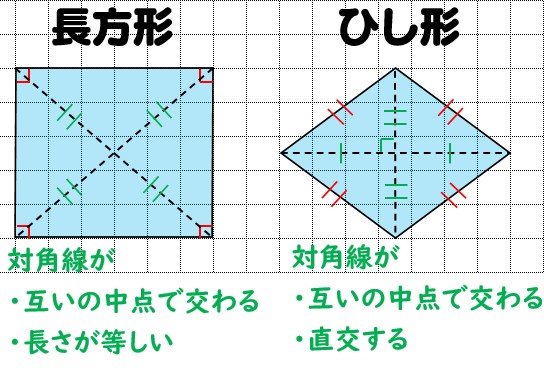
長方形,正方形,台形,平行四辺形,ひし形の対角線の長さや交わり方について,次のア, イ,ウにあてはまるものを選び, を書きましょう。 長方形 正方形 台形 平行四辺形 ひし形 ア 2本の対角線の長さ4 右の図の平行四辺形で,2本の対角線の交わった点をEとします。 ⑴ 直線AEの長さは何cmですか。 〔 〕 ⑵ 対角線BDの長さは何cmですか。 〔 〕 四角形の対 たい 角 かく 線 せん 向かい合った頂 ちょう 点 てん を結 むす んだ線を対角線といいます。 四角形に長方形・ひし形は平行四辺形の一種なので、平行四辺形の対角線の性質を持っています。 さらに、『すべての角が直角』の長方形と『すべての辺の長さが等しい』ひし形ですが、これらの定義とは対象的に対角線については長方形が 『対角線の長さが等しい』 、ひし形が 『対角線が直交する
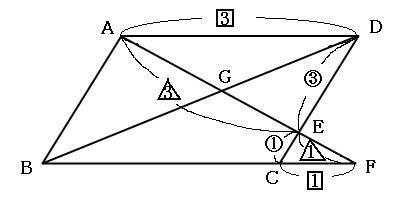



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
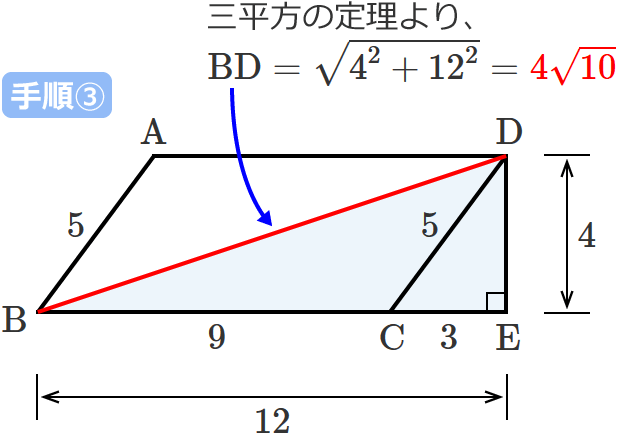



平行四辺形の対角線の長さの求め方
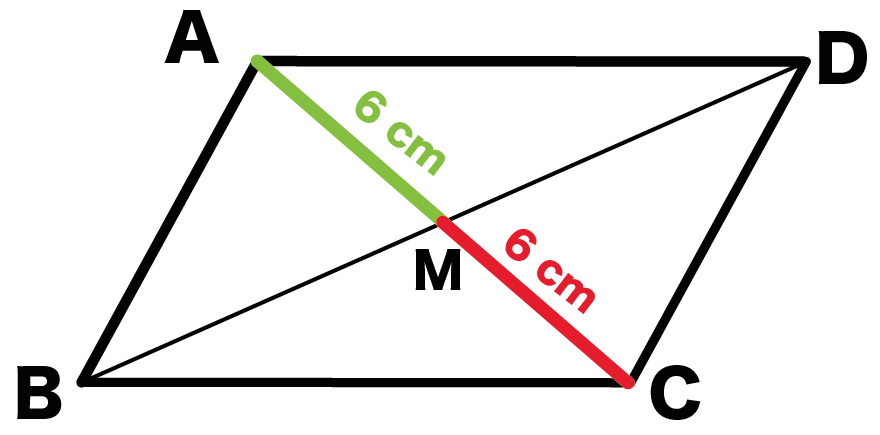
四角形は,1つの対角線で2つの三角形に分けることができます。 平行四辺形,ひし形,長方形,正方形は,1つの対角線で,形も 大きさも同じ2つの三角形に分けることができます。 trsA6F3tmpjtd 岩倉市日本語・ポルトガル語適応指導教室 平行四辺形には次の3つの性質があります。 1 平行四辺形では、2組の対辺はそれぞれ等しい 2 平行四辺形では、2組の対角はそれぞれ等しい 3 平行四辺形では、対角線はそれぞれの中点で交わる のどれかと勘違いしてませんか? https//mediaqikerume ①対角線の長さが等しい平行四辺形は長方形である。 ②対角線が垂直に交わる平行四辺形はひし形である。①、②のそれぞれ証明がわかりません。中学生レベルで教えて貰えませんか? 1)平行四辺形ABCDにおいて、対角線を引き、 ABCと BCDとして、平行四辺形の対辺は等しいわけだからAB=AC。BC



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
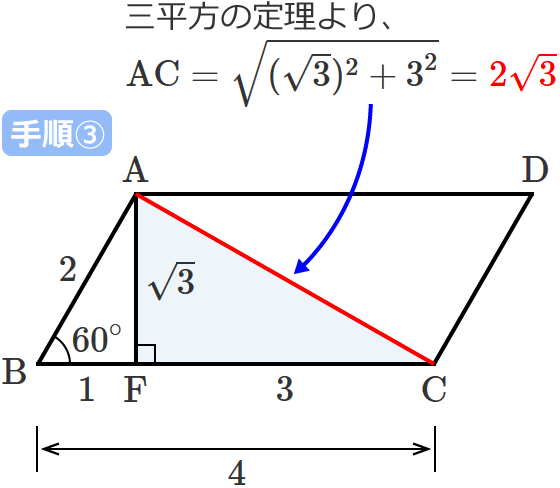



平行四辺形の対角線の長さの求め方
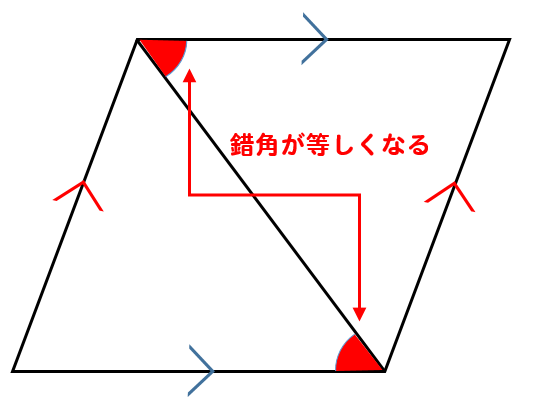
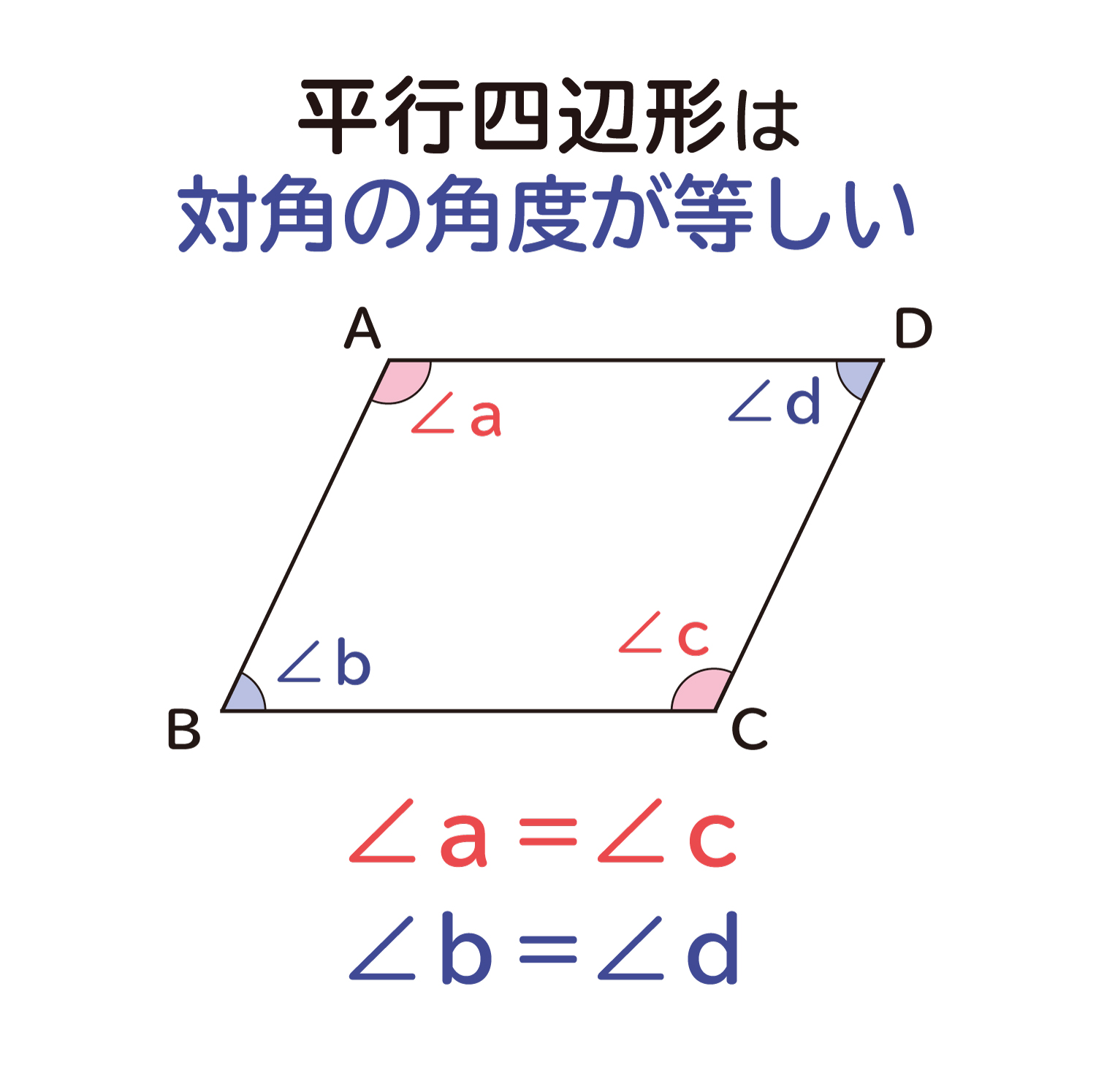
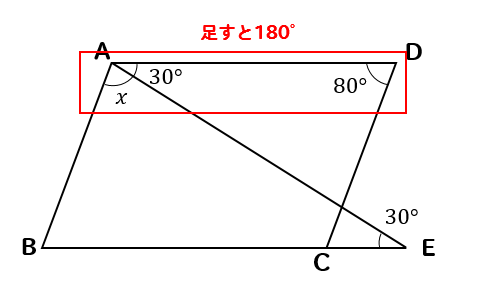
・平行四辺形には、下のような3つの性質があります。 1.対辺の長さが等しい 2.対角の角度が等しい 3.対角線は中点で交わる 今回、2つ目の平行四辺形の性質である、 対角の角度が等しい ことを確認していきたいと思います。形よりなる.実験条件刺激図形は,右下がりの対角線を持う9種の平行四辺形である.これらは,下 辺の長さが104ドット(長さ実験(0, 300) (303, 30帥ノ傾き=実験 (217レ350)バ3, 350)),平行四辺形 長方形 ひし形 正方形 二組の平行線で囲まれる図形(平行四辺形,長方形,ひし形,正方形)では隣り合う角の和は180°になります.台形(当脚台形も)はそうとは限りません. →閉じ




1 Abcd Descubre Como Resolverlo En Qanda




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
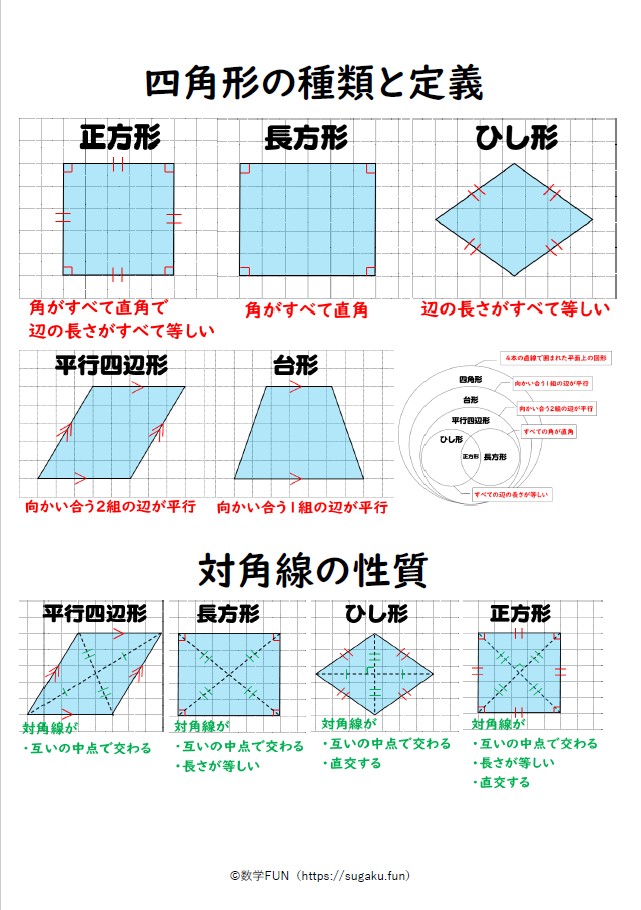
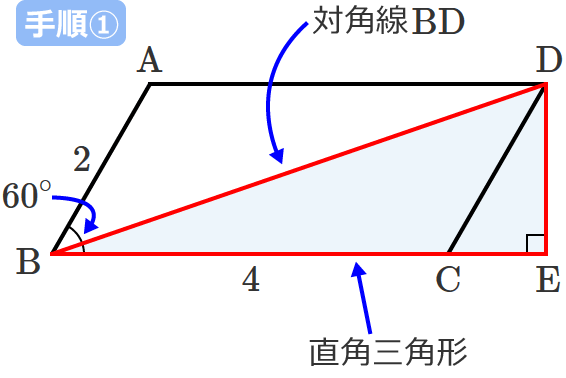
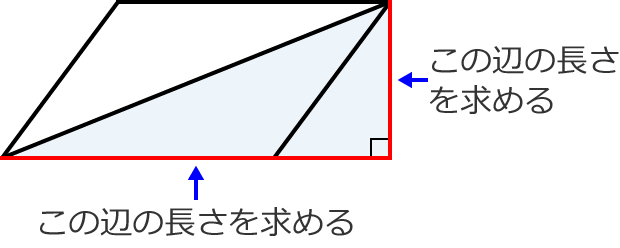
平行四辺形の「辺の長さ」と「高さ」から対角線の長さを求める 次のように、辺の長さと高さが分かっている平行四辺形 ABCD A B C D があるとします。 この平行四辺形の「対角線 BD B D の長さ」と「対角線 AC A C の長さ」を、先ほどの手順に従って求めてみます。平行四辺形では、対角線を引くと それぞれの中点で交わります。 厳選6パターンの問題に挑戦! それでは、平行四辺形の角度、辺の長さを求める問題をパターン別に解説していきます。 対角、対辺の基平行四辺形 ひし形 ① 2本の対角線の長さが等しい。 ( 正方形 )( 長方形 ) ② 2本の対角線が垂 すい 直 ちょく に交わる。 ( 正方形 )( ひし形 ) ③ 2 本の対角線が交わった点で、そ れぞれの対角線が2等分される。 ( 正方形 )( 長方形 )




ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
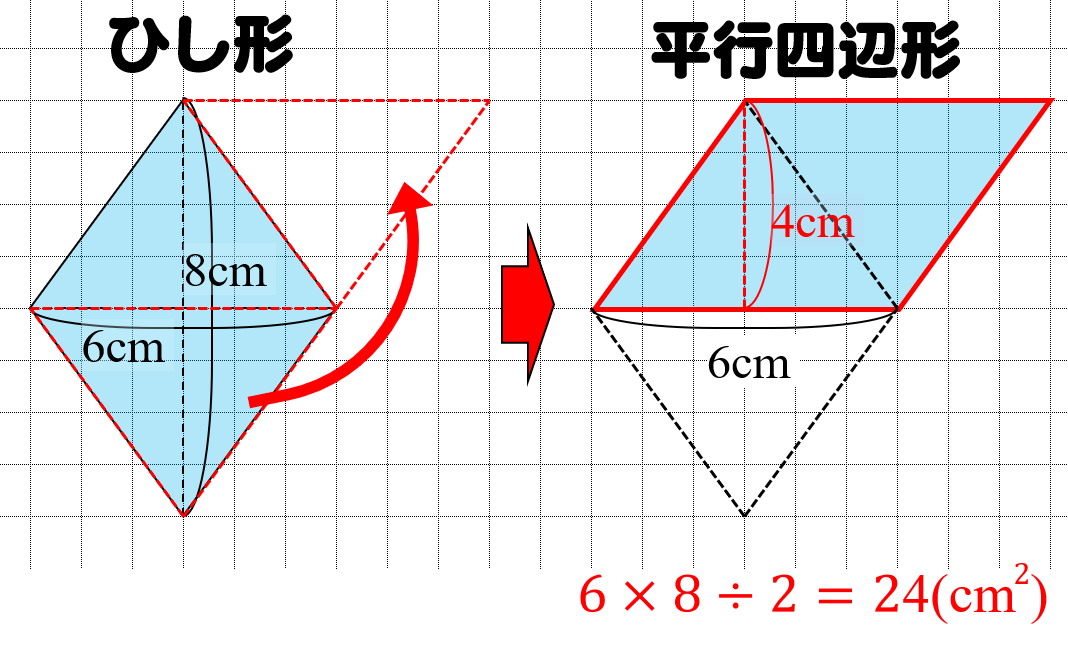



ひし形の面積の公式 小学生に教えるための分かりやすい解説 数学fun
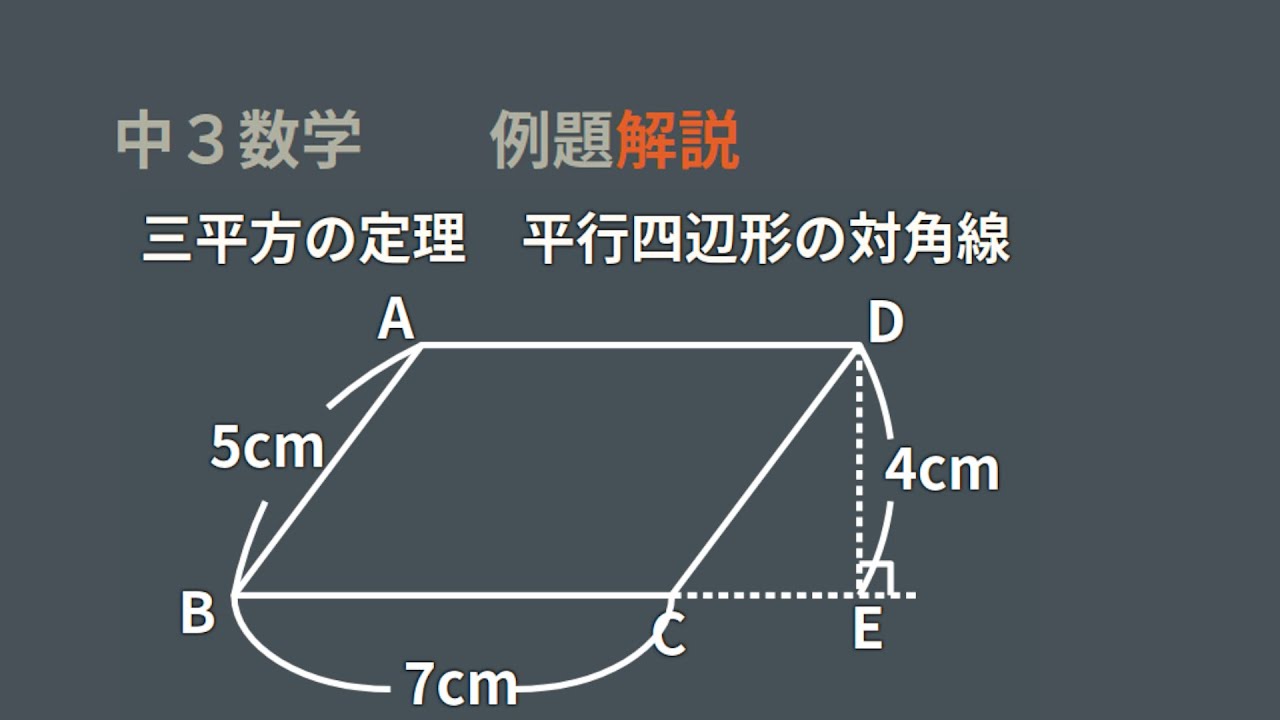
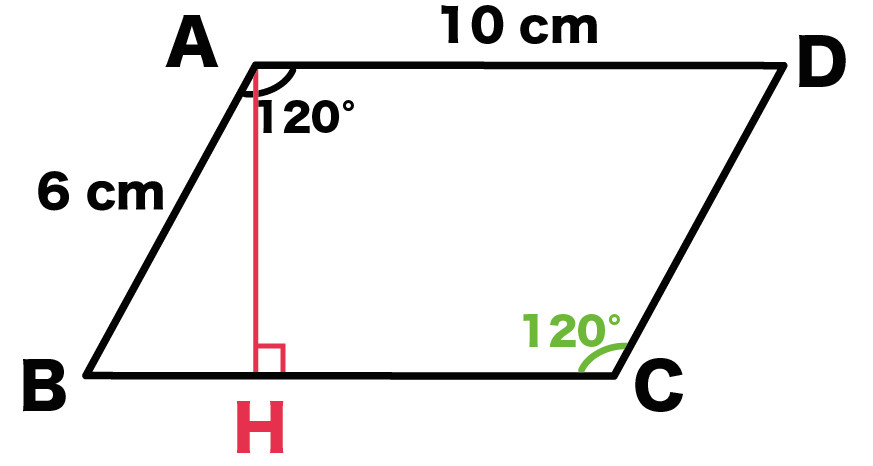
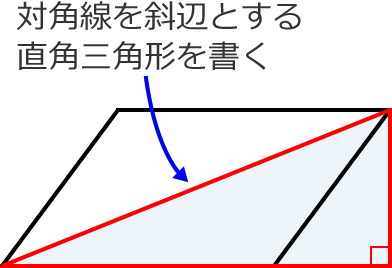
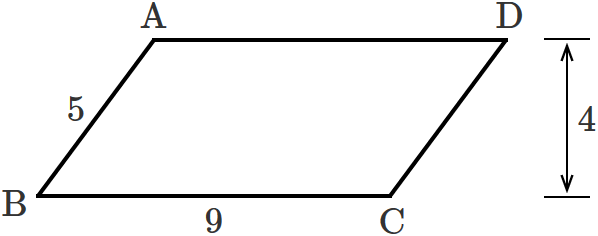
∠a=∠cbe(平行線になる条件) AB//DC AD//BC <戻る> 4 対角線が、それぞれの中点で交わる。 ABOと CDOで AO=CO 1 BO=DO 2 対頂角)3 1,2,3より2辺とその間の角がそれぞれ等しいので 中学数学 図形 平行四辺形とは? 定義・条件・性質や面積の公式、証明問題 21年2月19日 この記事では、「平行四辺形」の定義や条件、性質をできるだけわかりやすく解説していきます。 また、平行四辺形の面積の公式や、対角線の角度などの計算問題三平方の定理_平行四辺形の対角線 三平方の定理は直角三角形がなくては使えない。 図の中に直角三角形を見つけるか 補助線を書いて直角三角形を作ると解ける場合がある。 A B C D 4cm 5cm 7cm E ABCDはAB=5cm, BC=7cmである。 DからBCの延長線上に垂線を引き交点をEとする。 DE=4cmのとき 対角線ACと, 対角線BCの長さをそれぞれ求めよ。



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



平行四辺形で知っておくべきこと 苦手な数学を簡単に
平行四辺形の対角線の長さの求め方がわかる4ステップ 😂 Step3より、• 平行四辺形の成立条件その5:1組の対辺が平行であり、かつその長さが等しい 最後です。 10 平方四辺形を対角線で分けた $4$ つの三角形の面積は等しいから、平行四辺形の面積は、 $4\times \dfrac{3\sqrt{3}}{2} = 6\sqrt{3}$ だね! まとめ 平行四辺形の面積を対角線の長さと角度から求めるのに必要な特徴は、ユークリッド原論をどう読むか(3) 頁末 前 次 目次 ユークリッド原論 第1巻 命題1ー34(平行四辺形の対辺・対角・対角線) 平行四辺形・対角線 (平行四辺形と長斜方形とは同義) (平行四辺形の対角線は互いに他を2等分)



対角線で参観 教育考現学



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
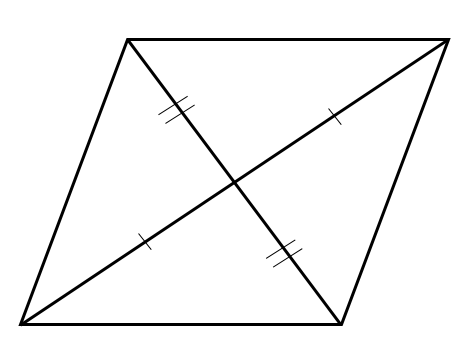
対角線 四角形の、向かい合う頂点同士をむすんだ直線のことを、対角線といいます。 ・2本の対角線が、それぞれのまん中の点で交わる四角形平行四辺形、ひし形、長方形、正方形 ・2本の対角線の長さが等しい四角形長方形、正方形 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 と言う条件が加われば、長方形になります。 平行四辺形の対角線の条件に、「 2本の対角線の長さが等しい 」 「 2本の対角線が垂直 ( 90° ) に交わる 」 と言う2つの条件が加われば、正方形になります。平行四辺形の定義と性質 定義 向かい合う2組の辺がそれぞれ平行な四角形 定理(性質) 2組の対辺がそれぞれ等しい 2組の対角がそれぞれ等しい 対角線がそれぞれの中点で交わる 定義は 「こういう四角形を平行四辺形としよう」 と決めたことなので




小学4年生の算数 台形 平行四辺形 ひし形 対角線 問題プリント ちびむすドリル 小学生



平行四辺形の二つの対角線の長さが違う理由って何ですか Aklv721 Yahoo 知恵袋
平行四辺形の角度を変えると 長方形になったよ。 「それでは、試してみますよ。」と言って、実物投影機に教具を映し出した。 平行四辺形の対角線の交わる角を、少しずつ90度に近づけていく。 少しずつ形が変わっていく平行四辺形を見ながら、




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生



平行四辺形 対角線




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の対角線は中点で交わる ことの説明 おかわりドリル




平行四辺形の面積の求め方 公式と計算例




平行四辺形の面積の求め方 公式と計算例




小5算数 平行四辺形が描けると 角の大きさがわかる ブログ アビット




対角線と四角形 Youtube



三平方の定理 平行四辺形の対角線



平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




無料 中2数学 標準問題 解答プリント 232 平行四辺形3 長方形とひし形




2 Ac15c1n Fc Cm 28 Descubre Como Resolverlo En Qanda




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典
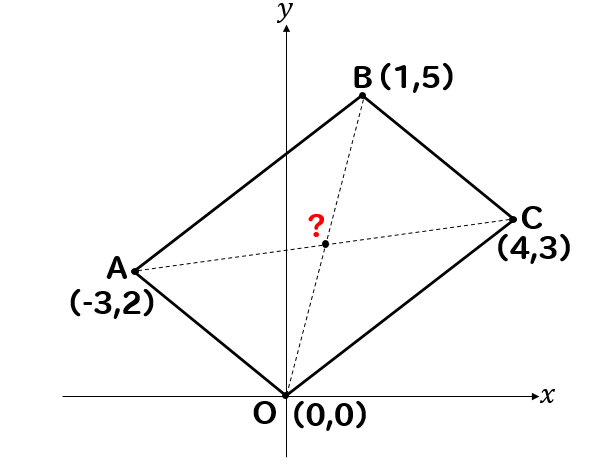



関数 グラフ上の平行四辺形の座標 面積 二等分線などの問題を解説 数スタ




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




平行四辺形の対角線の長さの求め方



1
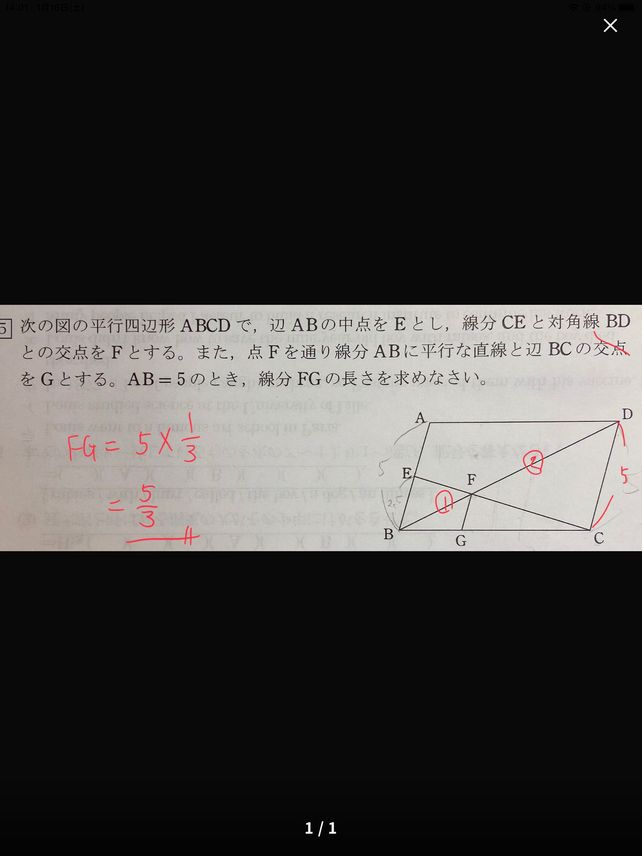



Abcd Ab E Ce Descubre Como Resolverlo En Qanda
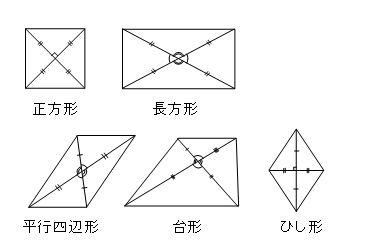



四角形の対角線 レッツスタディー




Acと は 同じ長さじゃないんですか Clear



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



1




平行四辺形の対角線の長さの求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




Math 平行四辺形 平行四辺形になることの証明 働きアリ



平行四辺形の対角の角度は等しくなる ことの説明 おかわりドリル




四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形の対角線の長さの求め方



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun



平行四辺形の対角線の長さの求め方



中2数学 平行四辺形の3つの性質 Qikeru 学びを楽しくわかりやすく




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室
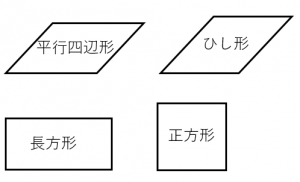



平行四辺形 ひし形 長方形 正方形の違い 具体例で学ぶ数学



平行四辺形の対角線の長さの求め方




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ




四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ



数i隣り合う2辺の長さが8 5でその間の角が60 である平行四辺形 Yahoo 知恵袋



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



1




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ



印刷 平行四辺形 対角線 角度 求め方 平行四辺形 対角線 角度 求め方



平行四辺形の対角線の角度について この条件の時の角度a Bを文字で表 Yahoo 知恵袋




これ 問題の中に1つも平行ってワードがないのに どうして中点連結定理になるのか そし Clear



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



平行四辺形 どんな四角形になるか 苦手な数学を簡単に




平行四辺形 Wikipedia




中2数学 平行四辺形の3大重要ポイント 映像授業のtry It トライイット



いろいろな四角形 四角形の対角線 シリウス 算数の学習指導案 授業案 教材 Edupedia エデュペディア 小学校 学習指導案 授業案 教材



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス




中2数学 平行四辺形の証明で知っておくべき5つの方法 映像授業のtry It トライイット




平行四辺形の面積を対角線の長さと角度から求める 解説図付き なぜか分かる はかせちゃんの怪しい研究室



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典



平行四辺形の対角線の長さの求め方



四角形の種類と定義 性質の違い 正方形 長方形 平行四辺形 ひし形 台形 数学fun




平行四辺形と長方形 ひし形 正方形の関係 苦手な数学を簡単に




平行四辺形のなかの三角形の相似や角度 長さ 等しい面積の求め方 現役塾講師のわかりやすい中学数学の解き方



平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



対角線の長さ 本数の求め方とは 公式を使って一瞬で計算しよう Studyplus スタディプラス



2




1 Abcd Descubre Como Resolverlo En Qanda




四角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




平行四辺形の性質 長さ 角度の問題 無料で使える中学学習プリント




無料の学習プリント 小学4年生の算数ドリル いろいろな四角形 みそにゃch




平行四辺形の辺や角を求める Youtube
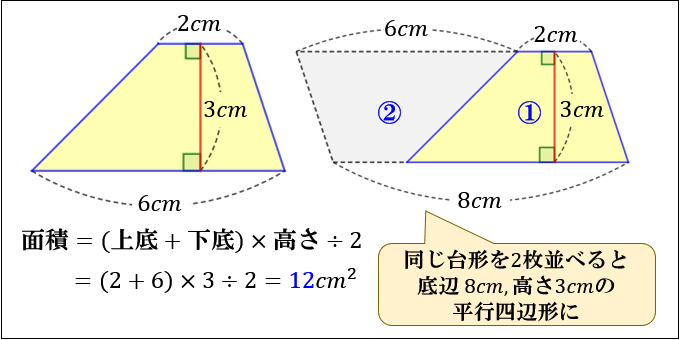



四角形の面積の求め方 公式とその仕組み 小学算数 アタリマエ




ボード 勉強 のピン




平行四辺形を中学生でもわかるように解説 性質 証明を即理解 高校生向け受験応援メディア 受験のミカタ




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ
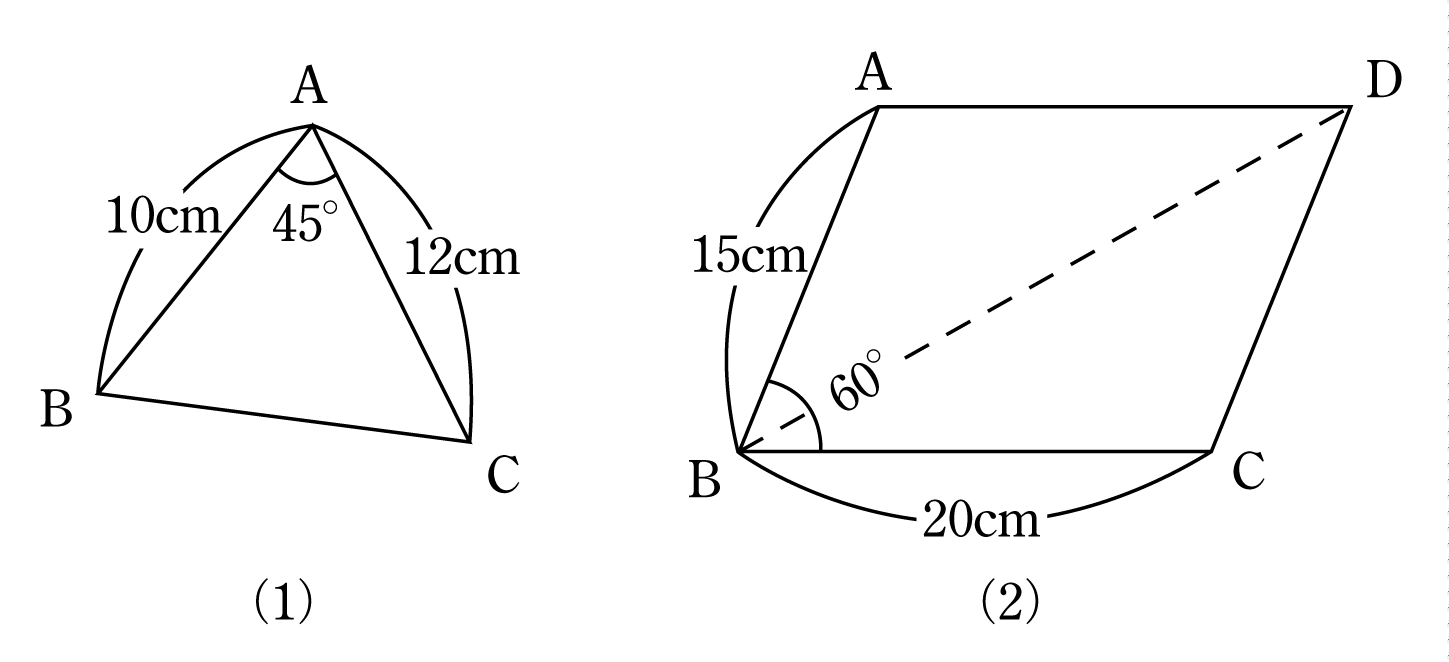



余弦定理と交流ベクトル計算への応用 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




ベスト 正方形 対角線 長さ ツール 正方形 対角線 長さ ツール Walljpxuanpat



高校物理の力の合成の問題です この平行四辺形の対角線の長さの求め Yahoo 知恵袋




長方形の性質 対角線の長さはなぜ等しいのか Qikeru 学びを楽しくわかりやすく



平行四辺形の3つの性質とその証明 具体例で学ぶ数学




平行四辺形の辺や角を求める Youtube




平行四辺形の角度 辺の長さ 求め方を問題解説 数スタ



平行四辺形の二つの対角線の長さが違う理由って何ですか Aklv721 Yahoo 知恵袋




中2数学 平行四辺形 長方形 ひし形 正方形の違い 映像授業のtry It トライイット



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー



ひし形の定義は 1分でわかる定義 正方形 平行四辺形との違い 対角線との関係
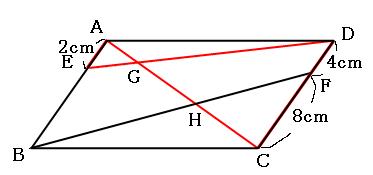



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ
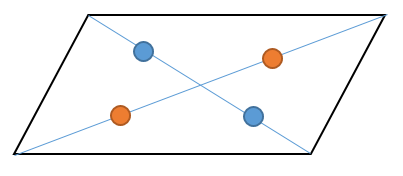



小学算数 平行四辺形 ひし形 長方形 正方形の対角線は真ん中で交わる 偏差値40プログラマー
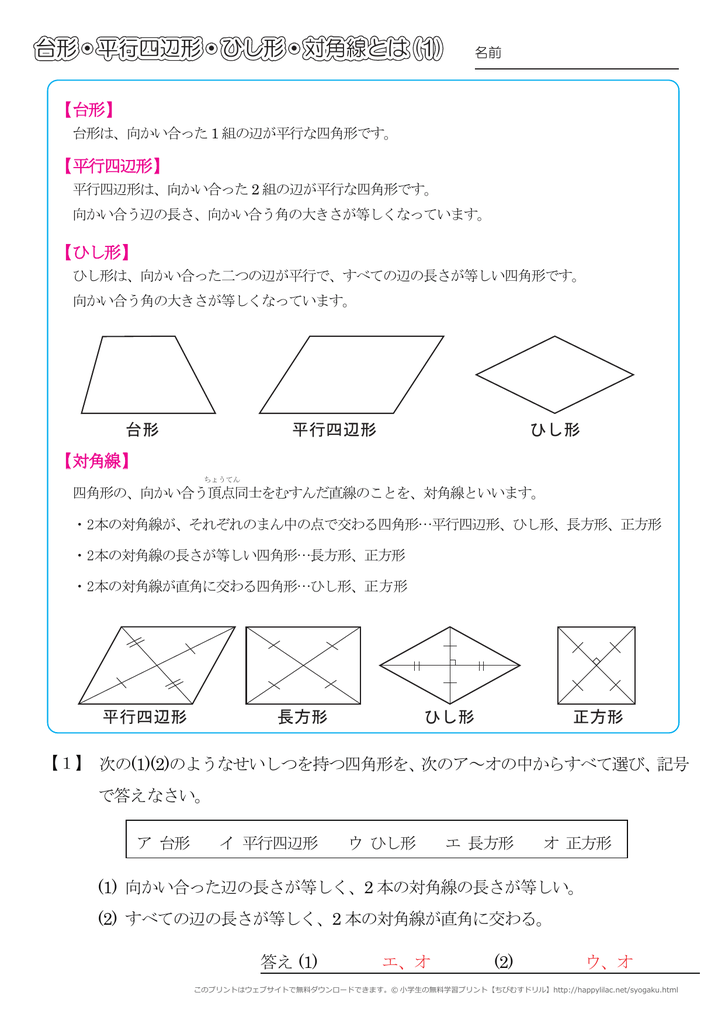



台形 平行四辺形 ひし形 対角線とは 1



平行四辺形とは 定義 条件 性質や面積の公式 証明問題 受験辞典




平行四辺形の定理や定義 平行四辺形の覚えておきたい性質は4つ 中学や高校の数学の計算問題




算数 小4 19 四角形の特ちょう Youtube
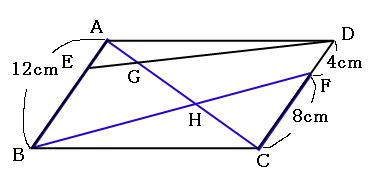



平行四辺形の対角線を3つに分ける問題を解くときはチョウチョを2匹探せ



平行四辺形の対角線の長さの求め方


